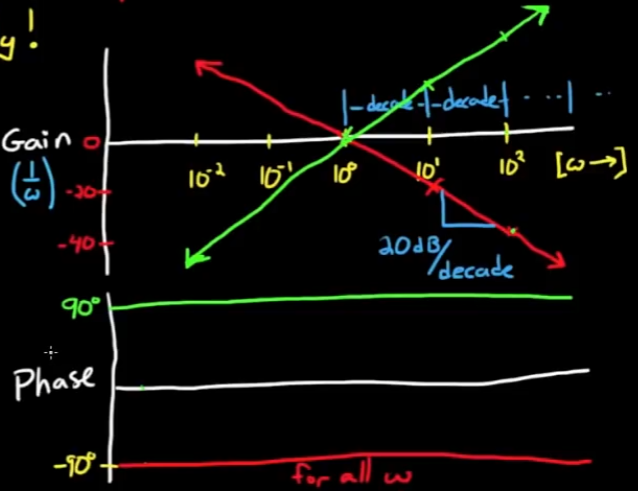
对于常数增益的系统, 即
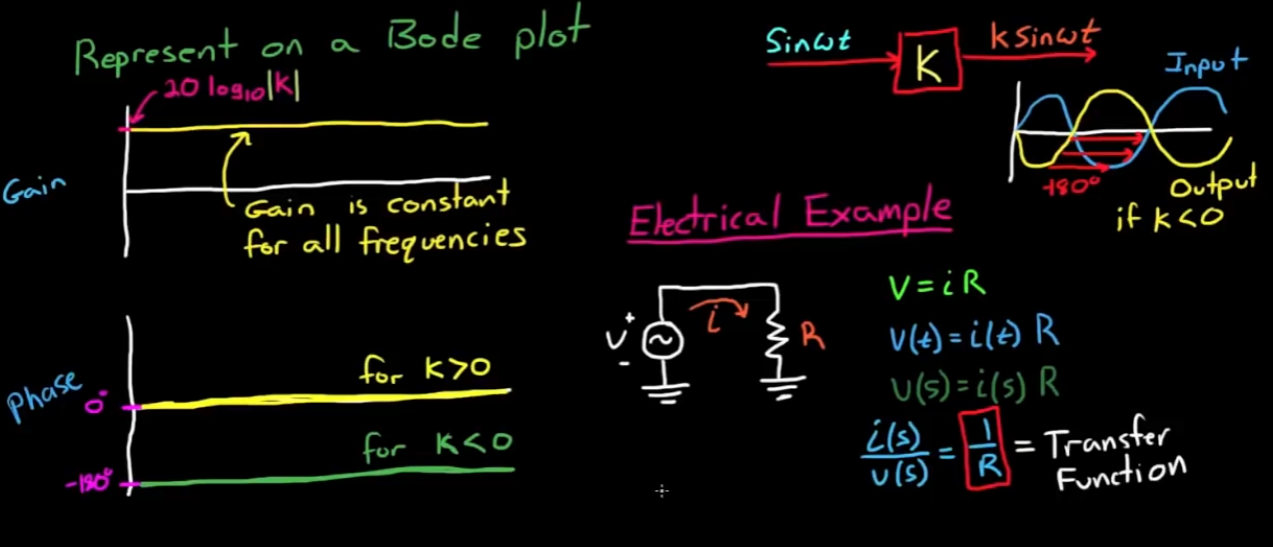
- 其频率响应H(s) = k. 将实部和虚部画在虚平面上, 增益永远为k, k > 0时, 向量与实轴夹角为0; k < 0时, 向量与实轴夹角为180°. 此时我们可以轻松地画出这个系统的bode图.
- 现在我们解锁了搭建复杂传递函数的第一个构件
对于零点和极点在原点处的系统, 即H(s) = s 和 H(s) = 1/s
- 零点, 即使H(s) = 0的s值, 当s = 0时H(s) = 0, 则称系统零点在原点处, 此时H(s) = s
- 极点, 即使H(s) = ∞的s值, 当s = 0时H(s) = ∞, 则称系统极点在原点处, 此时H(s) = 1/s
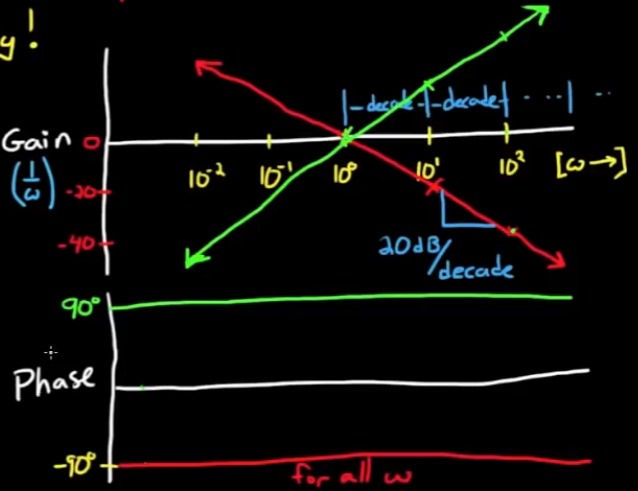
- 对于H(s) = 1/s, 即H(jω) = 1/jω, 在复平面上画出向量如图:
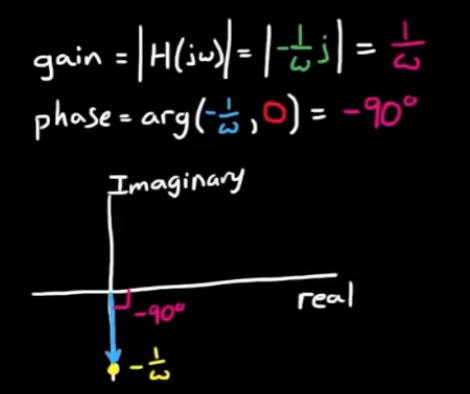
H(s) = 1/s实际上是一个积分器, 所以输入信号频率接近于0的时候增益无穷大
最终bode图如图:
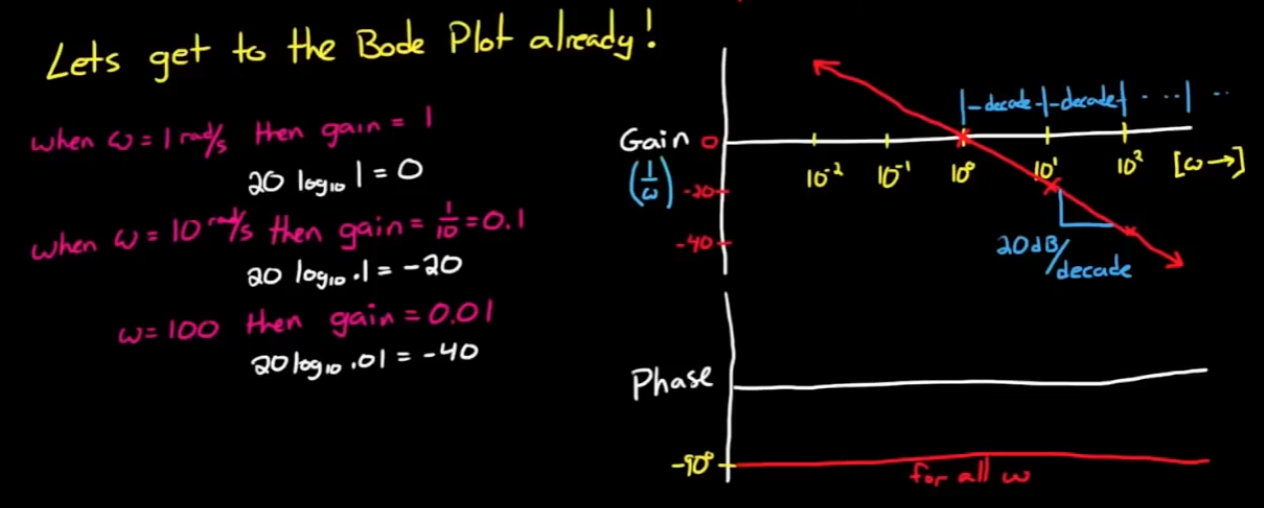
- 对于H(s) = s, 即H(jω) = jω, 它是一个微分器, 也就是积分器的逆运算, 所以积分器和微分器的增益, 相位应该相互抵消, 直接画出bode图如下:
- 对于更复杂的系统, 它的频率响应可以写成常数, 积分器, 微分器的乘积, 例如:

对于这种乘积的组合:
a. 考虑增益, 由于增益运算是对数, 所以增益的乘积可以转换成相加, 即将不同项的增益bode图相加
b. 考虑相移, 频域上的相乘等于时域上的卷积, u(t)卷(system A)卷(system B)卷…, 最后输出的信号是u(t)先经过A相移再经过B相移, 以此类推, 所以相移也应该是相加, 最后也是将不同项的相移bode图相加

- 再次考虑H(s) = s, 即H(jω) = jω, 可以写成H(jω) = 1/(1/jω), 所以可以理解为H(jω) = jω的响应是H(jω) = 1的响应减去H(jω) = 1/jω的响应, 也可以得到正确的bode图
- 现在我们解锁了搭建复杂传递函数的第二个构件
对于零极点在实轴上的系统, 即极点不直接在稳态响应的s = jω的平面上, 但是仍然会对稳态响应造成影响
- 一个有实极点的传递函数应该写成这样的形式:

其中ω_0被称为”转折频率”
不同的表达如下:
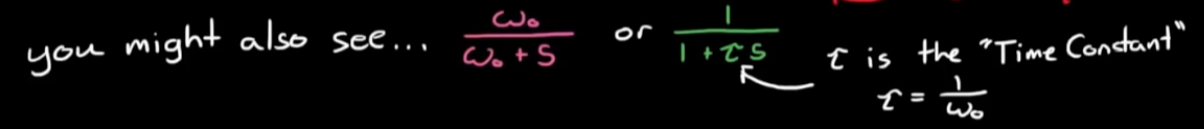
- 对于稳态响应, 设置s = jω, 由于我们需要得到函数的实部和虚部, 所以需要将其分开, 这里采用的是分母乘以共轭复数的形式:
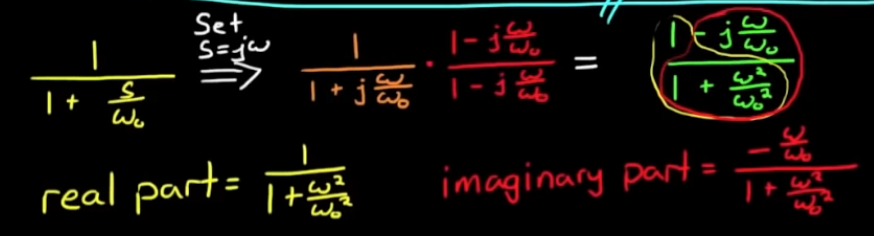
最终结果如下:
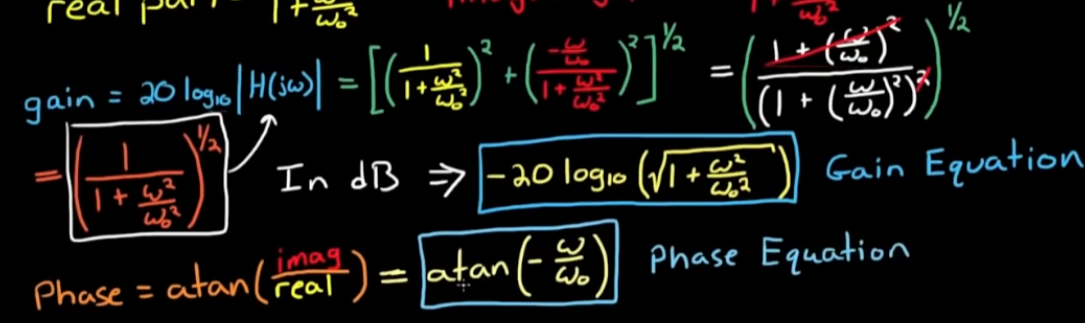
- 绘制bode图时, 先进行分段分析, 再来拟合.
a. 对于gain, 分析ω << ω_0, ω == ω_0, ω >> ω_0的情况
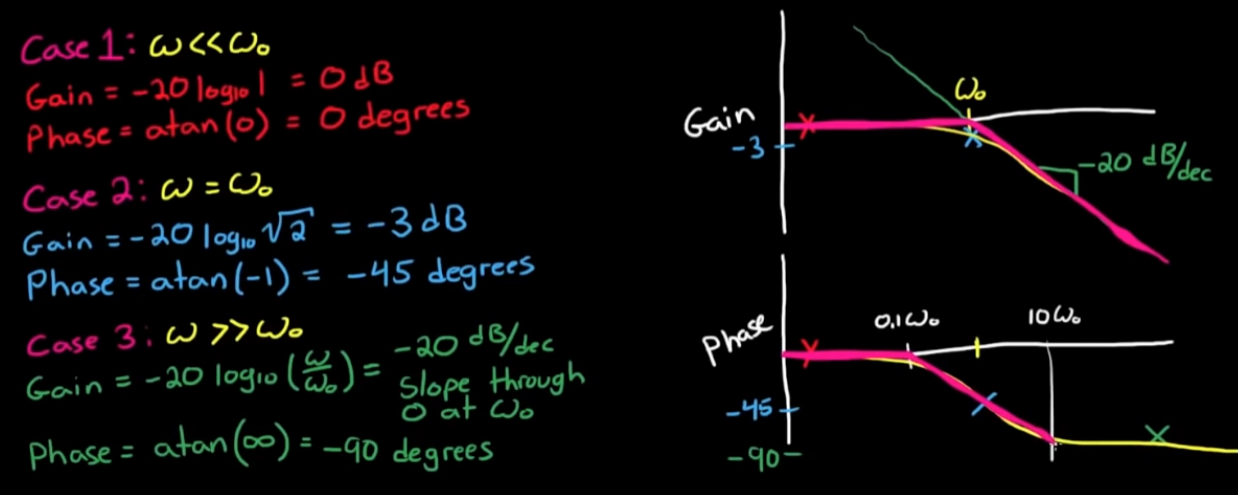
b. 对于phase, 分析ω << ω_0, ω == ω_0, ω >> ω_0的情况的基础上, 考虑ω稍大(ω == 10ω_0)和稍小(ω == 0.1ω_0)的情况, 得到中间段的变化规律如上图.
c. 从图中可以看出, 对于一个实极点系统, 可以通过两条直线估计其gain, 通过三条直线估计其phase, 转折频率ω_0这个参数至关重要. - 对于零点在实轴上的系统, 和分析零极点在原点时的思路一致, 我们也可以用有实极点系统的传递函数来表达有实零点系统的传递函数, 即:

则bode图如下棕色线部分:
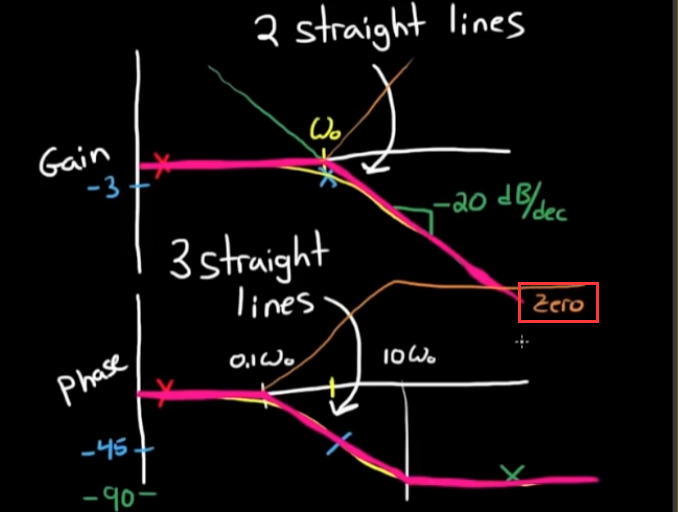
- 总结手绘实零极点系统bode图的方法: 对于”标准形式“的实零极点系统,
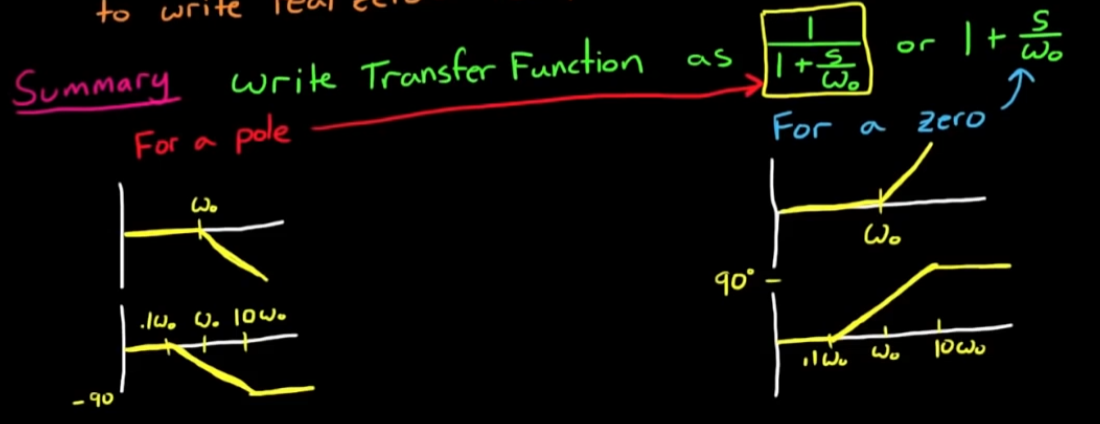
a. 考虑gain: 找到转折频率, 两条直线描绘, 其中斜线斜率为20dB/dec (横轴增大十倍, 变化20dB), 极点和零点图像对称
b. 考虑phase: 找到0.1ω_0, ω_0, 10ω_0的位置, 三条直线描绘, 极点和零点图像对称
c. 若系统不是”标准形式”, 采用线性运算使其变为”标准形式”, 例如:

- 现在我们解锁了搭建复杂传递函数的第三个构件
- 一个有实极点的传递函数应该写成这样的形式:
对于零极点是复数的系统,即落在s域4个象限上而不是轴上
- 复数极点和零点永远成对出现, 因为:
对于真实的物理系统, 要使一阶系统有复数极点, 则需要有一些物理参量含有虚数, 这是没有意义的;
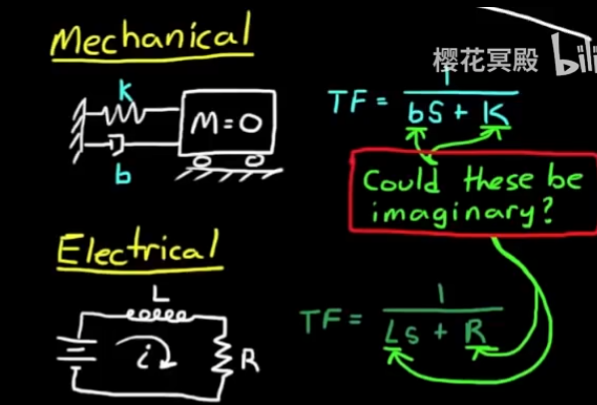
要使二阶系统有复数极点, 则可以用一个小学就学过的经典公式得到二次方程的根, 并且可以看出, 系统要不就是没有复极点, 要不就是有一对共轭复极点:

其中衡量b²与4ac的大小的一个系数被称为阻尼系数 damping ratio, 阻尼系数能直接暗示系统的响应是振荡运动还是指数衰减运动. - 进入数学阶段, 二阶系统的传递函数如下:

我们要想手绘bode图, 仍然是要把函数的实部和虚部分开求出, 然后通过数学方法或在虚平面上直观得到增益和相位.
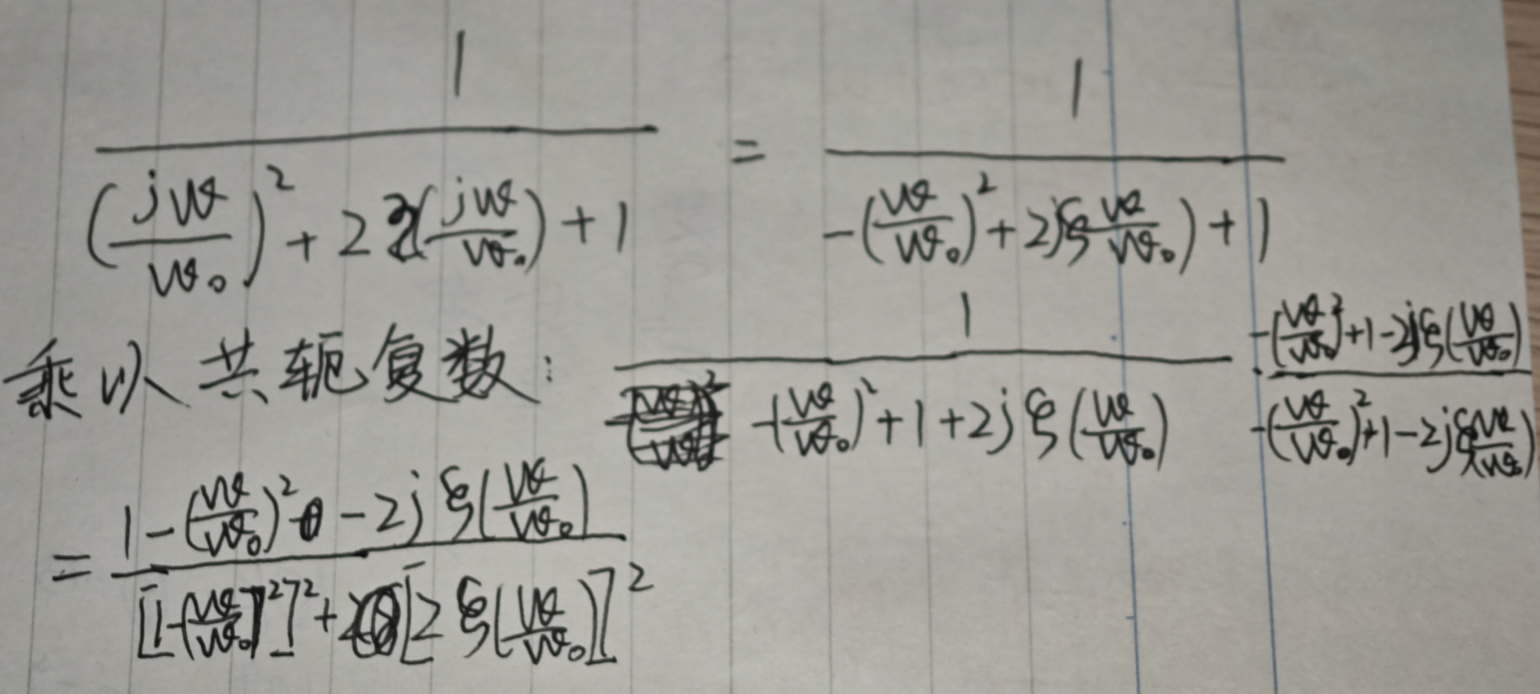

虽然相对复杂, 但是我们还是得到了实部和虚部. 仍然是分成ω << ω_0, ω == ω_0, ω >> ω_0三个部分来分析增益和相位:- ω << ω_0时
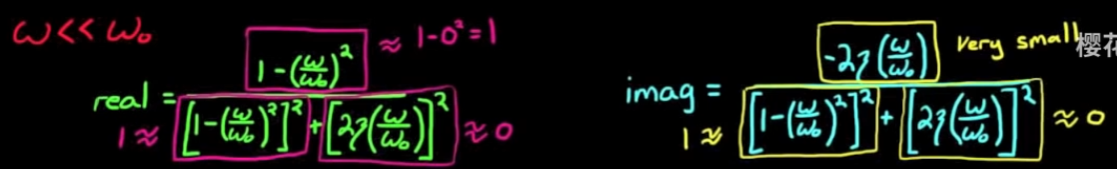
用数学方法和画图的方法都可以得到gain和phase:

- ω >> ω_0时
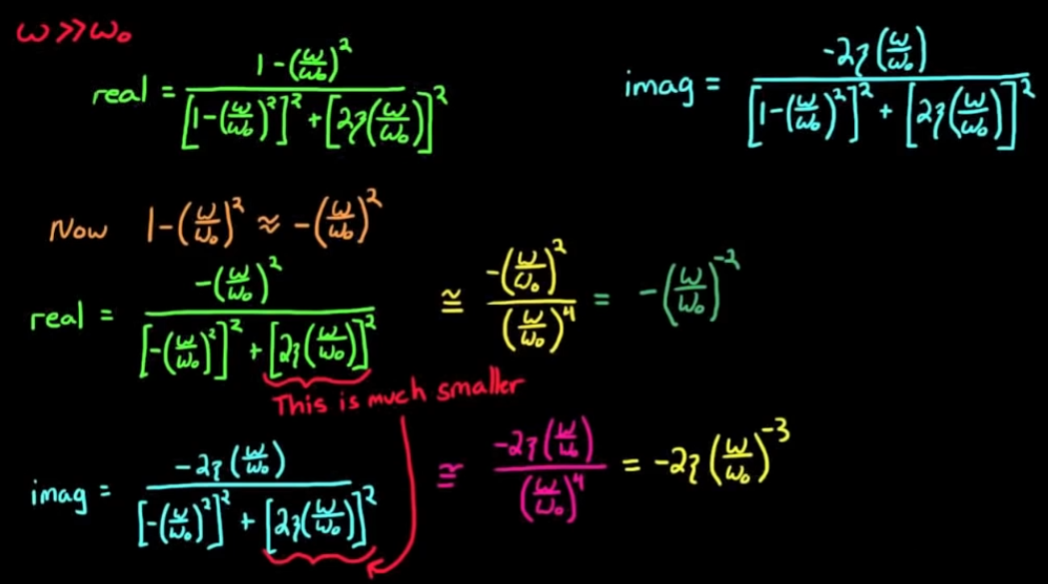
考虑gain, 近似为一条斜率为-40dB/decade的直线
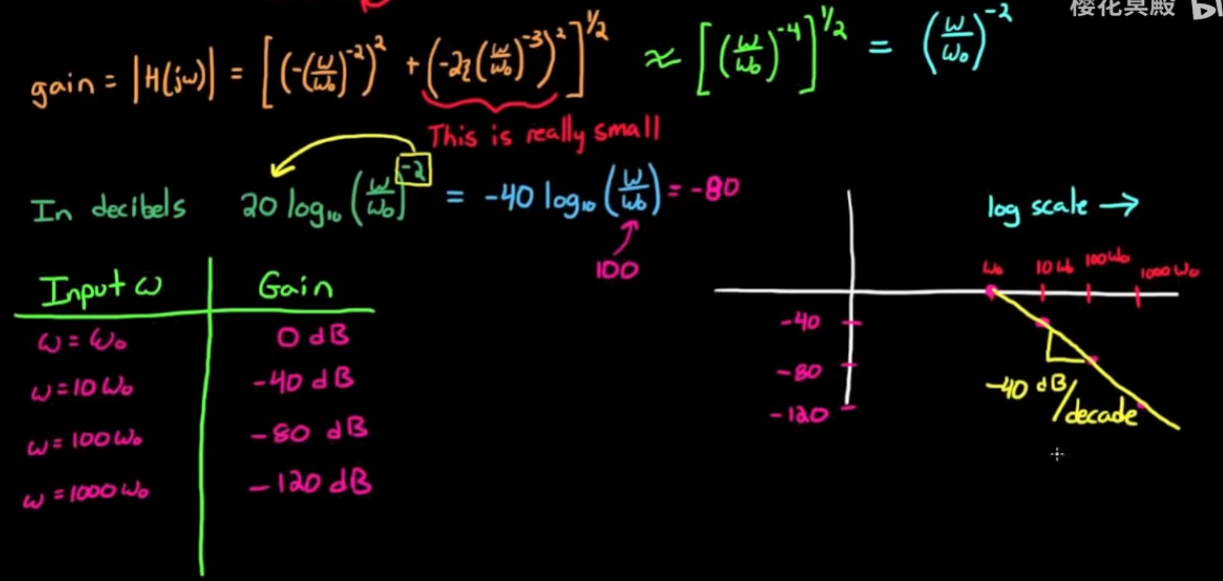
考虑phase, 由于实部和虚部都是负数, 虽然最后atan函数输出角度为0°, 但是实际phase是180°
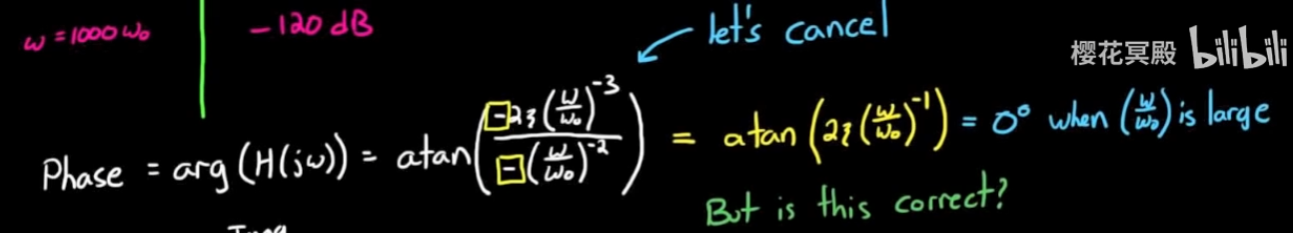
- ω == ω_0时, 需要分情况讨论, 先计算如下:
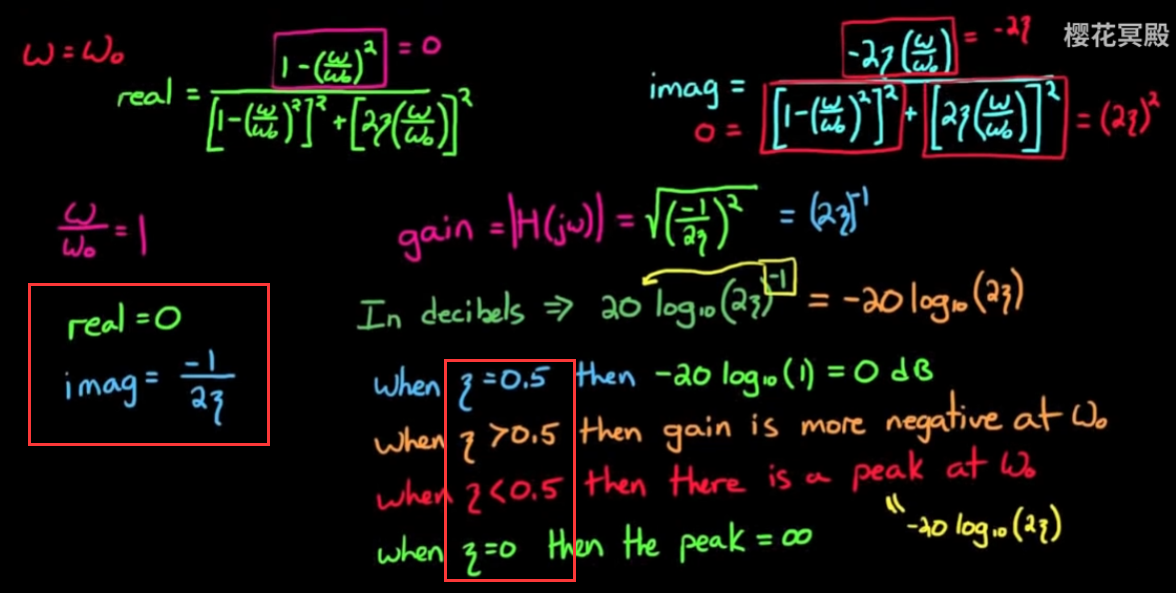
考虑gain, 如上图, damping ratio对bode图的形状起到了决定性作用:
= 0.5时, gain正好是0dB;
> 0.5时, gain在ω_0处会是一个负数;
< 0.5时, gain在ω_0处会有一个尖峰;
= 0, 也就是没有阻尼时, gain无穷大, 这符合直觉
考虑phase, 很简单
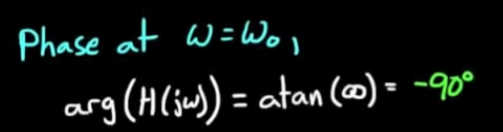
- ω << ω_0时
- 实际画出的bode图如下图
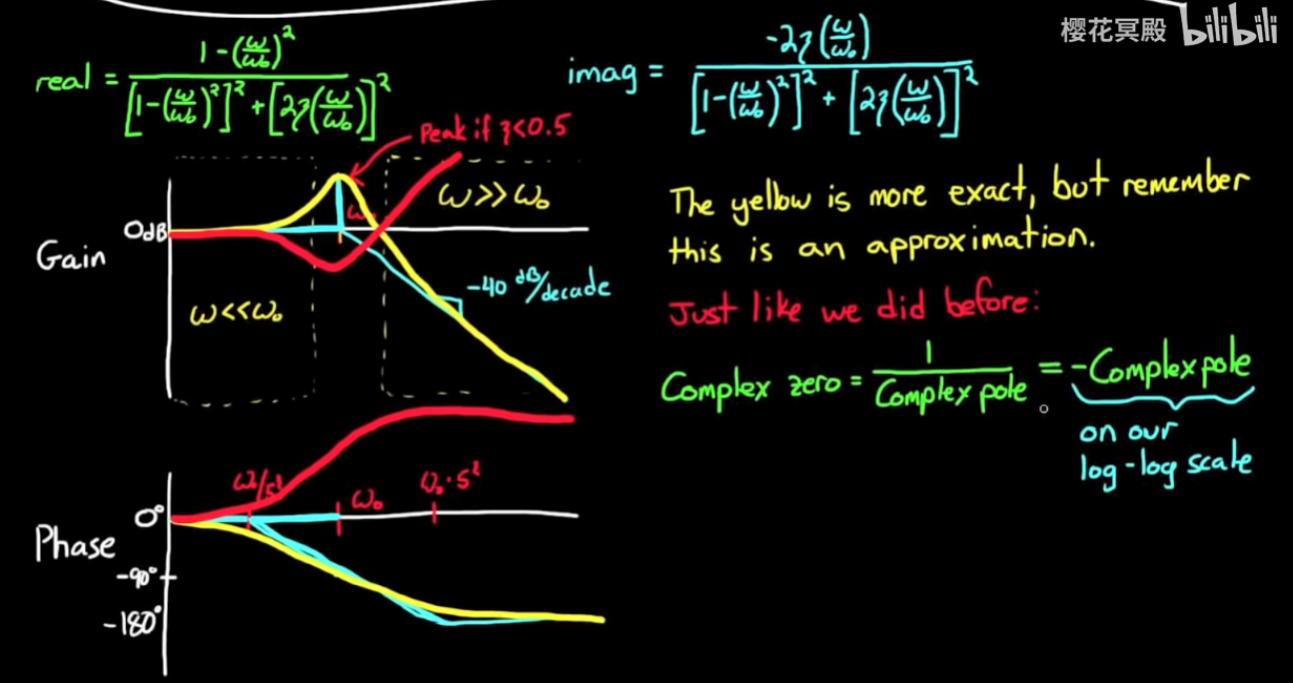
注意天蓝色为近似直线, 也就是我们之前分析的内容, 黄色为一对复极点的频响, 红色为一对复零点的频响. 复零点频响与复极点频响关于频率轴对称, 这一特性在之前的证明中已经反复提到. - 这样我们就得到了搭建复杂传递函数频响的所有构件.
- 复数极点和零点永远成对出现, 因为:
Bode图2 手绘bode图
分类:
日期:2025-03-26 21:25:15